平衡二叉树(AVL)介绍及其实现

一、平衡二叉树

　　任何一个数据的查找过程都需要从根结点出发，沿某一个路径朝叶子结点前进。因此查找中数据比较次数与树的形态密切相关。 对于二叉树来说，当树中每个结点左右子树高度大致相同时，树高为logN。则平均查找长度与logN成正比，查找的平均时间复杂度在O(logN)数量级上。当先后插入的关键字有序时，BST退化成单支树结构。此时树高n。平均查找长度为(n+1)/2，查找的平均时间复杂度在O(N)数量级上。

　　二叉查找树在最差情况下竟然和顺序查找效率相当，这是无法仍受的。事实也证明，当存储数据足够大的时候，树的结构对某些关键字的查找效率影响很大。当然，造成这种情况的主要原因就是BST不够平衡(左右子树高度差太大)。既然如此，那么我们就需要通过一定的算法，将不平衡树改变成平衡树。因此，AVL树就诞生了。AVL（Adelson-Velskii and Landis）树得名于它的发明者 G.M. Adelson-Velsky 和 E.M. Landis，他们在 1962 年的论文《An algorithm for the organization of information》中发表了它 。

　　在二叉树中，任何一个节点v的平衡因子都定义为其左、右子树的高度差。空树的高度定义为-1。在二叉查找树T中，若所有节点的平衡因子的绝对值均不超过1，则称T为一棵AVL树。维护平衡只需在插入和删除时维护平衡即可。

　　　　

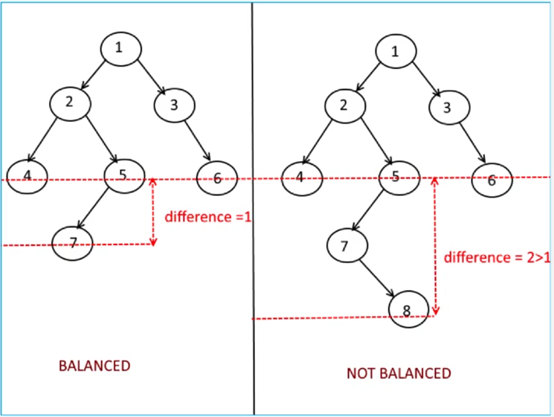
　　新节点记为N，第一个被破坏平衡的祖先记为p（至少是祖父），在同一路径上的p的子节点记为q，q的子节点记为s。按pqs的位置关系分为左左型，左右型，右右型，右左型，两两对称。通过旋转来使树重新平衡，旋转不会破坏BST的性质，也就是中序遍历的顺序，但能改变子树高度。

　　　　。

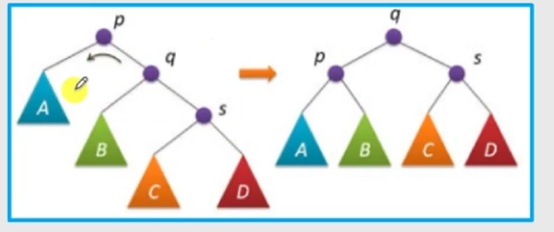　　旋转操作：旋转操作是一种调整树结构而不改变二叉查找树特性的手段。这里要理解树旋转的意义，树的最终目的不是维护节点与节点之间的层级关系，关键是如何用AVL树这种数据结构进行更好的查找和搜索。

　　　　

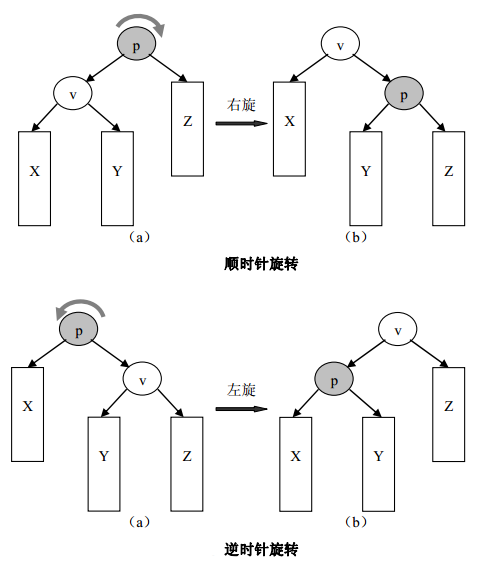
　　先看中间，左左型和右右型，它们只需沿反方向旋转一次即可。左右型和右左型，先调整q和s，转变为上述两种类型。念一下中序遍历顺序，找找感觉。

　　　

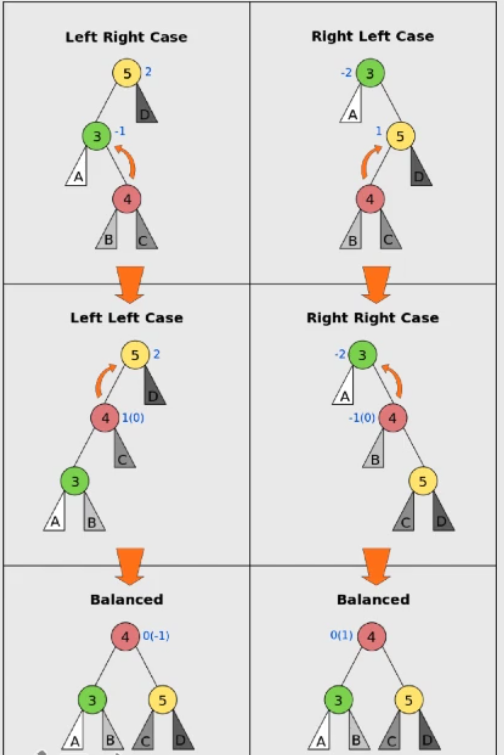
二、代码实现

　　AVL树是一棵二叉查找树，与普通二叉查找树不同的是，在插入和删除节点之后需要重新进行平衡，因此继承并重写普通二叉查找树的insert和remove方法，就可以实现一棵AVL树。代码里重点就是插入和删除怎样去维护平衡。

// 涉及到的类前面博客都有
public class AVLTree<K, V> extends BinarySearchTree<K, V> implements IBinarySearchTree<K, V> {
    @Override
    public BSTNode<K, V> insert(K key, V value) {
        // 先按bst的方式来插入，再调整
        BSTNode<K, V> nnode = super.insert(key, value);
        // 向上找到第一个不平衡的祖先p
        BSTNode<K, V>[] pqs = firstUnbalance(nnode);
        if (null != pqs) {// 不平衡
            // System.out.println(pqs[0].key);
            reBalance(pqs);
        }
        return nnode;
    }

    /* 分pqs的形状，来调用左旋和右旋 */
    private void reBalance(BSTNode<K, V>[] pqs) {
        if (pqs == null)
            return;
        BSTNode p = pqs[0];// 不平衡的那个祖先
        BSTNode q = pqs[1];// p的子节点
        BSTNode s = pqs[2];// q的子节点

        if (q.isRight() && s.isRight()) {// 右右型，以p为中心逆时针旋转
            leftRotate(p, q);  // 方法在前面的博客
            // reBalance(firstUnbalance(q));
        } else if (q.isLeft() && s.isLeft()) {// 左左型，以p为中心顺时针旋转
            rightRotate(p, q);
            // reBalance(firstUnbalance(q));
        } else if (q.isLeft() && s.isRight()) {// 左右型
            // q.right = s.left;
            // if (s.left != null) {
            // s.left.parent = q;
            // s.left.isLeftChild = false;
            // }
            // q.parent = s;
            // s.left = q;
            // q.isLeftChild = true;
            //
            // s.parent = p;
            // p.left = s;
            // s.isLeftChild = true;
            leftRotate(q, s);// q，s左旋，变为左左型
            rightRotate(p, s);
            // reBalance(firstUnbalance(s));
        } else {// 右左型
            // q.left = s.right;
            // if (s.right != null) {
            // s.right.parent = q;
            // s.right.isLeftChild = true;
            // }
            // q.parent = s;
            // s.right = q;
            // q.isLeftChild = false;
            //
            // s.parent = p;
            // p.right = s;
            // s.isLeftChild = false;
            rightRotate(q, s);
            leftRotate(p, s);
            // reBalance(firstUnbalance(s));
        }
    }

    private BSTNode<K, V>[] firstUnbalance(BSTNode<K, V> n) {
        if (n == null)
            return null;
        BSTNode s = n;
        BSTNode p = n.parent;
        if (p == null)
            return null;
        BSTNode g = p.parent;
        if (g == null)
            return null;
        if (unBalance(g)) {// 不平衡了
            return new BSTNode[] { g, p, s };
        } else {
            return firstUnbalance(p);
        }

    }

    @Override
    public void remove(K key) {
        BSTNode<K, V> node = super.lookupNode(key);
        if (node == null)
            return;

        BSTNode<K, V> parent = node.parent;
        BSTNode<K, V> left = node.left;
        BSTNode<K, V> right = node.right;

        if (left == null && right == null) {// leaf node
            super.removeNode(node);
            reBalance(parent);    // 重新平衡
        } else if (right == null) {// has only left child.左孩子替换自身
            // if (node.isLeft()) {
            // parent.left = left;
            // left.parent = parent;
            // } else {
            // if (parent == null) {// node is root
            // left.parent = null;
            // root = left;
            // } else {
            // parent.right = left;
            // left.isLeftChild = false;
            // left.parent = parent;
            // }
            // }
            BSTNode<K, V> predecessor = maxNode(left);
            BSTNode<K, V> parentOfPredecessor = predecessor.parent;
            super.removeNode(predecessor);
            node.key = predecessor.key;
            node.value = predecessor.value;
            reBalance(parentOfPredecessor);

        } else {// 有右孩子,找到右子树的最小
            BSTNode<K, V> successor = minNode(right);
            BSTNode<K, V> parentOfSuccessor = successor.parent;
            // minNode must be leaf node
            super.removeNode(successor);
            node.key = successor.key;
            reBalance(parentOfSuccessor);
        }
    }

    private void reBalance(BSTNode<K, V> node) {
        if (node == null)
            return;

        BSTNode<K, V> right = node.right;
        BSTNode<K, V> left = node.left;
        int hOfRight = getHeight(right);
        int hOfleft = getHeight(left);

        if (hOfRight - hOfleft >= 2) {// 右侧高
            leftRotate(node, right);// 左旋
            reBalance(right);
        } else if (hOfRight - hOfleft <= -2) {
            rightRotate(node, left);
            reBalance(left);
        } else {
            reBalance(node.parent);
        }
    }
}